Louis Poinsot

Louis Poinsot (1777–1859) was a French mathematician and physicist. Poinsot was the inventor of geometrical mechanics, showing how a system of forces acting on a rigid body could be resolved into a single force and a couple.

Contents

Life

"Everyone makes for himself a clear idea of the motion of a point, that is to say, of the motion of a corpuscle which one supposes to be infinitely small, and which one reduces by thought in some way to a mathematical point."
--Louis Poinsot, Théorie nouvelle de la rotation des corps (1834)

Louis was born in Paris on January 3, 1777. He attended the school of Lycée Louis-le-Grand for secondary preparatory education for entrance to the famous École Polytechnique. In October 1794, at age 17, he took the École Polytechnique entrance exam and failed the algebra section but was still accepted. A student there for 2 years, he left in 1797 to study at École des Ponts et Chaussées to become a civil engineer. Although now on course for the practical and secure professional study of civil engineering, he discovered his true passion, abstract mathematics. Poinsot thus gave up civil engineering and left the École des Ponts et Chaussées to become a mathematics teacher at the secondary school Lycée Bonaparte in Paris, from 1804 to 1809. From there he became inspector general of the Imperial University of France where he shared a post with another famous mathematician Delambre. On November 1, 1809, Poinsot became assistant professor of analysis and mechanics at his old school the École Polytechnique.

During this period of transitions between schools and work, Poinsot had remained active in research and published a number of works on geometry, mechanics and statics so that by 1809 he had an excellent reputation (see Works).

By 1812 Poinsot was no longer directly teaching at École Polytechnique using substitute teacher Reynaud, and later Cauchy, and lost his post in 1816 when they re-organized, but he did become admissions examiner and held that for another 10 years. He also worked at the famous Bureau des Longitudes from 1839 until his death.

On the death of Joseph-Louis Lagrange in 1813, Poinsot was elected to fill his place at the Académie des Sciences. In 1840 he became a member of the superior council of public instruction. In 1846 he was awarded an Officer of the Legion of Honor, and on the formation of the Senate in 1852 he was chosen a member of that body. Poinsot was elected Fellow of the Royal Society of London in 1858. He died in Paris on December 5, 1859.

From the diary of Thomas Hirst, December 20, 1857:

"..[Poinsot] shook me kindly by the hand, bid me be seated, and took his seat near me. He is now between 60 and 70 years old, with silver silken hair neatly arranged on a fine intelligent head. He is tall and thin, but although he now stoops with age and feebleness one can see that one time his figure was more than ordinarily graceful. He was loosely but neatly dressed in a large ample robe de chambre. His features are finely moulded - indeed everything about the man betokens good blood. He talks incessantly and well. I did not misunderstand a word, although he spoke always in a low tone, and now and then his voice dropped as if from weariness, but he never wandered from his point ..."

The crater Poinsot on the Moon is named after him. A street in Paris is called Rue Poinsot (14th Arrondissement). When Gustave Eiffel built the famous tower, he included the names of 72 prominent French scientists on plaques around the first stage, Poinsot included.

Work

"Poinsot was determined to publish only fully developed results and to present them with clarity and elegance. Consequently he left a rather limited body of work ..."
--Dictionary of Scientific Biography (see Sources)

Works include:

Poinsot was the inventor of geometrical mechanics, which showed how a system of forces acting on a rigid body could be resolved into a single force and a couple. Previous work done on the motion of a rigid body had been purely analytical with no visualization of the motion, and the great value of the work, as Poinsot says, it enables us to represent to ourselves the motion of a rigid body as clearly that as a moving point (Encyclopædia Britannica, 1911). In particular he devised, what is now known as, Poinsot's construction. This construction describes the motion of the angular velocity vector 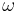\mathbf{\omega} of a rigid body with one point fixed (usually its center of mass). He proved that the endpoint of the vector 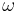\mathbf{\omega} moves in a plane perpendicular to the angular momentum (in absolute space) of the rigid body.[1]

He discovered four new regular polyhedra, in 1809, two of which appear in Kepler's work of 1619, although Poinsot was unaware of this. There are only four Kepler-Poinsot polyhedra, the other two are the great icosahedron and great dodecahedron, some people call these two the Poinsot solids. In 1810 Cauchy proved, using Poinsot's definition of regular, that the enumeration of regular polyhedra is complete. In 1990 a mistake was discovered in Poinsot's and Cauchy's definition when an internal inconsistency was discovered..

Poinsot worked on number theory studying Diophantine equations. However he is best known for his work in geometry and, together with Monge, regained geometry's leading role in mathematical research in France in the 19th century. Poinsot also contributed to the importance of geometry by creating a chair of advanced geometry at the Sorbonne in 1846. Poinsot created the chair for Chasles which he occupied until his death in 1880.

References

  1. ^ E.T. Whittaker, Analytic Dynamics of Particles and Rigid Bodies, Cambridge UP, 4th edition, (1938), p. 152 ff.

Sources

External links

 This article incorporates text from a publication now in the public domain: Chisholm, Hugh, ed (1911). Encyclopædia Britannica (11th ed.). Cambridge University Press.